Last week I participated (and co-organised) the 103rd European Study Group with Industry (normally abbreviated as ESGI) in Lyngby, Denmark. ESGI is a workshop where companies propose real problems from their industry which have mathematical flavour – and where mathematicians attempt to solve these problems. In connection to the 103rd ESGI there was a summer school with the title “Modern Methods in Industrial Mathematics”. The summer school had lectures and exercises in fractional calculus, operations research and optimal control.
For the workshop, four industry problems were proposed:
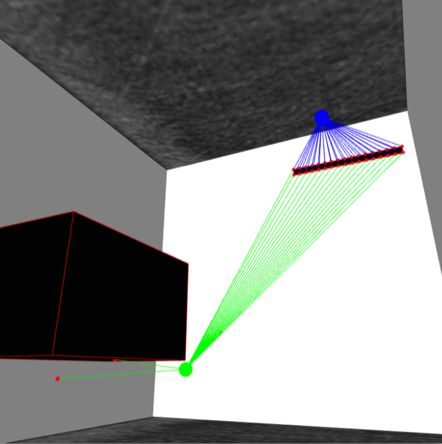
- Sensor positioning in electrical cabinets: A company producing electrical components were producing sensors which shut off the power if an electrical arc appears in a cabinet. The sensors which detect such arcs have to be positioned within the cabinet, and they wanted to determine optimal sensor positions when the cabinets included obstacles.
- Calibrating gyroscopes for side-mirror rotation: This company were producing a hardware/software solution for rotating the side mirror on large trucks, such that the mirror always faced the right way when the trucks were turning. Two gyroscopes were used for measuring the angle of rotation – but gyroscopes have a tendency to drift quite a lot. They wanted a way to reduce the amount of drift using accelerometer data.
- Modelling water flow in a root-screening facility: A grass-producing company wanted to dynamically control water levels in a facility for testing root-depth. They wanted to use a set of valves and sensors to have a complex water saturation structure in the soil.
- Algorithm optimisation for optimal robot accelerations: A company producing robots wanted to optimise one of their algorithm for moving robot arms. When a robot arm with many joints received a new instruction on where to move, it calculated an optimal way to turn the joints to follow a path there. Each joint has a maximum rotational torque, and their algorithm for determining how to rotate the joints while obeying torque constraints was too slow.
I worked on the first problem of optimally placing light sensitive sensors within an electrical cabinet. The problem we faced looks somewhat similar to the Art Gallery Problem, but the 3-dimensional cabinets make the problem quite a bit less trivial to solve. We developed and implemented algorithms which placed sensors optimally in 3d cabinets like the one shown below:
This was my fifth study group with industry, and it was an immense pleasure as always. There are in particular two things which I think ESGI makes very clear:
Real math is very hard: When studying a degree in mathematics, one rarely gets to work on real problems. Most of the “real” problems that is encountered throughout the years of studying are the nicest examples of real problems to be found, where they are often picked since they highlight some theory which perfectly solve the problem. In reality, many problems are either intractable, solvable by rather simple math or simply a test of ones skills in understanding the details of the asked problem.
Everybody have something to offer: What surprised me a lot at my first study group is that senior researchers and young students both have a lot to offer when it comes to solving industrial problems. The young students often have fresh perspectives on the problems and superior coding skills, where senior people have a load of experience with mathematical modelling. It is an amazing experience to throw away the normal hierarchies and work together; bachelor students, PhD students and professors.
For an overview of future study groups, see this site: www.maths-in-industry.org